2019 A Level H2 Chemistry Paper 1 Question 19 - Friedel Crafts Acylation of Methylbenzene

Let Chemistry Guru, Singapore's renowned JC Chemistry tuition centre, guide you through 2019 A Level H2 Chemistry Paper 1 Question 19.

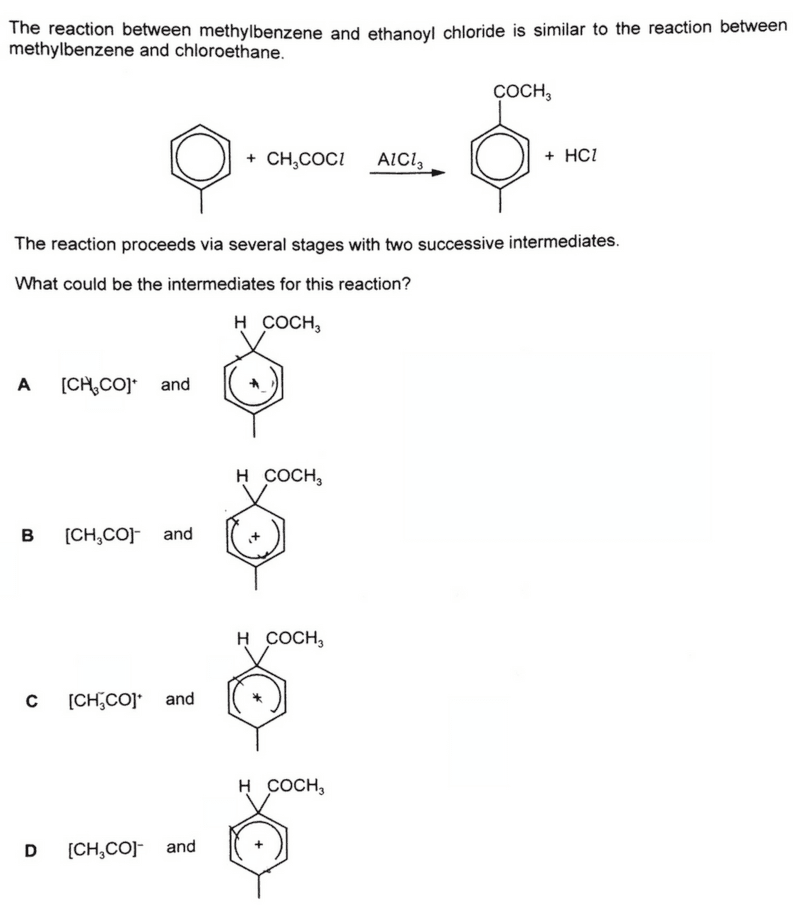
2019 p1 q19 question

We are required to predict the intermediates for the Friedel Crafts Acylation reaction.

This reaction is not in syllabus but we can apply what we know from the mechanism of electrophilic substitution for benzene to figure out the intermediates.

If you are not familiar with electrophilic substitution mechanism, do check out this video lesson that I've done previously.

Let's draw out the mechanism part by part.

1. Generate Electrophile

2019 p1 q19 generate electrophile

AlCl3 acts as a Lewis Acid and accepts electron pair from Cl- (of acid chloride) to form carbocation intermediate [CH3CO]+ and AlCl4-

The carbocation acts as the electrophile which will attract benzene which is electron rich.

Hence looking at the options we can eliminate B and D where the [CH3CO]- intermediates are negatively charged.

2. Electrophilic Attack

2019 p1 q19 electrophilic attack on methylbenzene

Benzene will use its delocalised pi system to attack the [CH3CO]+ intermediate and form a highly unstable intermediate.

Notice the [CH3CO]+ electrophile is added to position 4 with respect to methyl group since alkyl groups are 2,4-directing.

Also, the benzene carbon that is attached to the -COCH3 group is sp3 hybridised or saturated.

Hence the region around that sp3 carbon has no delocalisation of pi electrons, and we have to draw the "ring opening" around that carbon.

So we will eliminate option D where the "ring opening" is around methyl group.

Finally we can conclude the answer to this question is option A.

Topic: Arenes, Organic Chemistry, A Level Chemistry, Singapore

Back to list of questions for 2019 A Level H2 Chemistry Paper 1

Found this A Level Chemistry video useful?

This free chemistry video lesson is brought to you by Chemistry Guru, Singapore's top H2 Chemistry tuition choice since 2010.

Please like this video and share it with your friends!

Join my 18,000 subscribers on my YouTube Channel for new A Level Chemistry video lessons every week.

Check out other A Level Chemistry Video Lessons here!

Need an experienced tutor to make Chemistry simpler for you?

Do consider signing up for my JC Chemistry Tuition classes at Bishan or online tuition classes!